La programmation avec OpenGL sous Windows
Date de publication : 11 janvier 2010
III. Les bases d'OpenGL
III-A. Introduction
III-B. La projection et la rastérisation
III-C. Les buffers
III-D. Récupérer des informations
III-E. Les matrices
III-F. Paramétrage de la vue
III-F-1. Généralités
III-F-2. La fenêtre de visualisation (viewport)
III-F-2-a. Théorie
III-F-2-b. Application
III-F-3. La projection
III-F-3-a. Introduction
III-F-3-b. Projection orthographique
III-F-3-c. Projection en perspective
III-F-3-d. La correction de perspective
III-F-4. Le repère
III-F-5. Tout est relatif
III-F-5-a. Le repère et les objets
III-F-5-b. Le repère et la caméra
III-G. Dessiner
III-G-1. Généralités
III-G-1-a. Les vertices
III-G-1-b. Les couleurs
III-G-1-c. Le test de profondeur
III-G-2. Les primitives
III-G-2-a. Points (GL_POINTS)
III-G-2-b. Lignes (GL_LINES, GL_LINESTRIP et GL_LINE_LOOP)
III-G-2-c. Polygones
III-G-2-c-i. Cas général : GL_POLYGON
III-G-2-c-ii. GL_TRIANGLES
III-G-2-c-iii. GL_TRIANGLE_STRIP
III-G-2-c-iv. GL_TRIANGLE_FAN
III-G-2-c-v. GL_QUADS
III-G-2-c-vi. GL_QUAD_STRIP
III-G-3. Conclusion
III. Les bases d'OpenGL
III-A. Introduction
Cette partie est la plus théorique de toutes, car c'est ici que vous allez réellement commencer à apprendre la programmation avec OpenGL. Le fait qu'elle soit théorique ne signifie pas qu'elle
est inutile. Au contraire, c'est bien la partie la plus importante de ce tutoriel ! Sans cette partie, ce document ne serait qu'une collection de codes sources que
vous allez probablement réutiliser/modifier sans forcément tous les comprendre. Une fois que vous aurez terminé cette partie, vous verrez que le reste n'est qu'un jeu d'enfants.
Pour être bien préparé pour cette partie, oubliez carrément un instant la programmation. Préparez vous plutôt à faire un tout petit peu ... de maths.
III-B. La projection et la rastérisation
Vous dessinez avec OpenGL en utilisant des commandes que vous lui en envoyez à l'aide des fonctions associées. Comme les objets que vous dessinez sont en 3D
(vous pouvez également dessiner des objets 2D mais ce n'est qu'un cas particulier de la 3D) alors que l'écran est plat, ces objets sont d'abord converties en 2D
pour l'écran (c'est la projection) puis rastérisés (c'est-à-dire pixelisés) avant d'effectivement être affichés à l'écran. En effet, les coordonnées 3D et 2D utilisées par OpenGL
lors des calculs sont des coordonnées "réelles", alors que l'écran n'a pas une résolution aussi élevée, d'où la nécessité de la rastérisation (conversion des coordonnées
2D réelles en coordonnées 2D d'écran). Les algorithmes de conversion de coordonnées 3D en coordonnées 2D ne nous regardent pas mais il faut juste savoir qu'elles ont évidemment
lieu avant l'affichage des résultats.
Après la rastérisation, l'image n'est pas encore réellement "plate", mais composée de fragments. Les fragments sont des objets qu'on pourrait décrire approximativement par
la structure C suivante :
typedef struct _FRAGMENT {
int x, y;
FCOLOR Color;
double DepthIndex;
FRANG Rang;
} FRAGMENT;
|
Les fragments sont donc en quelque sorte des "candidats au titre de pixel". Lorsqu'un pixel a plusieurs postulants, OpenGL doit faire un choix : lequel de tous ces candidats doit être
définitivement promu en pixel. Ce choix en fait, c'est vous qui lui indiquerez comment le faire. La plupart du temps vous lui direz de choisir le fragment le plus proche du premier plan.
Vous pourrez également ajouter des règles supplémentaires, etc., nous y reviendrons plus tard. Lorsque tous les fragments ont été testés, l'image 2D finale prête à être envoyée à l'écran
est formée. Ce test n'a lieu que lorsque l'affichage du rendu est demandé (via glFlush par exemple).
III-C. Les buffers
OpenGL stocke les informations de fragments, entre autres, dans ce qu'on appelle des buffers. Par exemple, les informations de couleur sont stockés dans le color buffer et les informations
de profondeur (z-order) dans le depth buffer, appelé encore z-buffer. Vous pouvez réinitialiser tous les bits d'un buffer à l'aide de la fonction glClear. Par exemple, pour réinitialiser tous les
bits du color buffer (c'est-à-dire réinitialiser la couleur de chaque fragment) vous écrivez glClear(GL_COLOR_BUFFER_BITS) et si vous voulez également réinitialiser en même temps les bits du z-buffer
(c'est-à-dire réinitialiser le z-order de chaque fragment), vous écrivez glClear(GL_COLOR_BUFFER_BITS | GL_DEPTH_BUFFER_BITS). Avant chaque actualisation d'une scène, il est donc évident que vous devez
toujours commencer par réinitialiser les buffers sinon les fragments qui n'ont pas subi de changement garderont leurs anciennes valeurs ce qui pourrait perturber le processus de projection.
Maintenant nous-nous posons la question : avec quelle valeur les bits des buffers sont-ils réinitialisés ?
Dans le cas du color buffer par exemple, la valeur utilisée est celle que vous avez spécifiée à l'aide de la fonction glClearColor, par défaut 0.
void glClearColor(GLclampf red, GLclampf green, GLclampf blue, GLclampf alpha);
|
GLclampf est un type défini par OpenGL. C'est un type flottant dont le nom rappelle que la valeur que vous entrez sera mappée vers une autre. Dans le cas des couleurs par exemple, les valeurs "clamp" 0.0 et 1.0
d'une composante (c'est-à-dire qu'il s'agisse de R, de G, de B ou de A) sont respectivement mappées vers les valeurs entières 0 et 255. Ainsi, si vous voulez utiliser le bleu comme couleur à utiliser dans glClear, vous écrivez :
glClearColor(0.0, 0.0, 1.0, 0.0).
Pour les autres buffers, nous en reparlerons plus tard, mais le principe est strictement le même.
III-D. Récupérer des informations
Pour demander une information à OpenGL, on utilise le plus souvent "glGet". En fait, glGet n'est pas une fonction mais le nom générique donné à un groupe de fonctions dont les plus élémentaires étant glGetBooleanv, glGetIntegerv,
glGetFloatv et glGetDoublev.
void glGetBooleanv(GLenum param_name, GLboolean *param_values);
void glGetIntegerv(GLenum param_name, GLint *param_values);
void glGetFloatv(GLenum param_name, GLfloat *param_values);
void glGetDoublev(GLenum param_name, GLDouble *param_values);
|
Il est aisé de constater qu'il existe une version pour chaque type de donnée de base. Le résultat est retourné dans un buffer à passer en paramètre car l'information peut parfois être un tableau. Par exemple, pour obtenir la couleur
actuellement utilisée avec glClearColor, vous devez passer un tableau de 4 GLint, GLfloat ou GLdouble à la fonction appropriée en spécifiant GL_COLOR_CLEAR_VALUE dans le premier paramètre. Le v en fin du nom de chaque fonction
vient d'ailleurs de vector, c'est-à-dire vecteur ou tout bêtement tableau. Cette décoration de noms en fonctions des paramètres attendus est une pratique très utilisée dans OpenGL.
Il existe encore d'autres fonctions "glGet", comme glGetError qui permet de connaître le code d'erreur de la première erreur non testée par exemple, mais nous n'en reparlerons que le moment où nous aurons besoin d'elles.
III-E. Les matrices
Les matrices sont un formidable outil mathématique permettant de simplifier de nombreux calculs numériques. OpenGL utilise les matrices pour calculer le résultat d'une projection (conversion 3D vers 2D), d'une transformation (rotation,
homothétie, translation, etc.) et pour bien d'autres choses encore. Toutes les matrices d'OpenGL sont des matrices 4 x 4, représentées par des tableaux de flottants remplies par colonne. Ainsi, à titre illustratif, le tableau suivant :
GLfloat A = {a0, a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15};
|
Représente la matrice :
[a0 a4 a8 a12]
[a1 a5 a9 a13]
[a2 a6 a10 a14]
[a3 a7 a11 a15]
|
Dans OpenGL, il existe 3 matrices :
- La matrice de projection, utilisée pour calculer le résultat d'une projection
- La matrice de changement de repère, utilisée pour les changements de repère et donc aussi pour les transformations
- Et la matrice de gestion des textures, qui nous intéresse peu.
OpenGL utilise des piles de matrices (une par matrice, ce qui fait qu'il y en a trois) afin de ne jamais avoir à calculer des inverses. Une pile, si vous ne vous êtes jamais servi, est une structure de type LIFO (Last Input, First Output),
c'est-à-dire que le dernier élément qu'on a empilé (fait entrer) est le premier que l'on pourra dépiler (faire sortir). Dans OpenGL, on sélectionne une matrice avec la fonction glMatrixMode. Les constantes que vous pouvez utiliser en unique paramètre
de cette fonction sont GL_PROJECTION, GL_MODELVIEW et GL_TEXTURE. Vous avez sûrement deviné le rôle de chacune. Ainsi, pour sélectionner la matrice de projection par exemple, vous écrivez glMatrixMode(GL_PROJECTION). Tant que vous n'avez
pas encore appelé glMatrixMode, c'est la matrice GL_MODELVIEW qui est sélectionnée. Utilisez "glGet"
pour connaître la matrice actuellement sélectionnée (GL_MATRIX_MODE) ou encore pour lire une matrice que vous identifierez par GL_PROJECTION_MATRIX, GL_MODELVIEW_MATRIX ou par GL_TEXTURE_MATRIX, selon évidemment la matrice que
vous voulez lire.
Les fonctions suivantes permettent de manipuler la matrice sélectionnée :
glPushMatrix(void);
void glPopMatrix(void);
void glLoadMatrixf(const GLfloat *m);
void glLoadMatrixd(const GLdouble *m);
void glLoadIdentity(void);
void glMultMatrixf(const GLfloat *m);
void glMultMatrixd(const GLdouble *m);
|
III-F. Paramétrage de la vue
III-F-1. Généralités
Le paramétrage de la vue fait intervenir la notion de repère, de caméra, de volume de visualisation et de fenêtre de visualisation (viewport).
Le monde dans lequel vous dessinez est un espace orienté par un repère orthogonal direct (Oxyz). Au démarrage d'OpenGL :
- La fenêtre de visualisation est égale à la plus grande surface initialement disponible (c'est-à-dire pour nous qui sommes sous Windows, égale à la zone cliente initiale de notre fenêtre)
- L'origine O du repère se trouve au centre de la fenêtre de visualisation (en fait, cela est vrai dans la quasi-totalité des implémentations mais n'est précisée nulle part dans la specification originale de OpenGL)
- Les axes x, y et z sont respectivement orientées vers notre droite, vers le haut et vers nous
- La caméra est placée à l'origine du repère et tournée vers le sens négatif de l'axe z, la tête du cameraman pointant vers le sens positif de l'axe y.
- Les plans d'équations x = -1, x = 1, y = -1 et y = 1 délimitent la fenêtre de visualisation. Plus précisément, le volume de visualisation est le cube limité par les plans d'équations x = -1, x = 1, y = -1, y = 1,
z = -1 et z = 1. Cela est également un détail d'implémentation largement utilisé. La spécification originale ne précise rien de pareil.
Les deux derniers points peuvent être à priori contradictoires. Ils méritent que l'on médite un peu dessus. En effet, nous avons dit que la caméra est initialement placée en (0, 0, 0) et qu'elle regarde dans le sens négatif de l'axe z.
Alors si on place un point en (0, 0, -0.5) par exemple, la caméra la verra ou pas ? Elle la vera ! C'est-à-dire que ce point apparaîtra sur notre fenêtre de visualisation. Pourquoi ? Parce que ce point est bien contenu dans le champ de vision
(ou volume de visualisation) de la caméra ! Bien entendu, aucune caméra réelle ne peut avoir un champ de vision aussi grand, ni un champ de vision en forme de parallélépipède. Alors comment définir un volume de visualisation plus proche de la réalité ?
Les paragraphes suivants justement introduisent les notions qu'il faut avoir pour savoir bien paramétrer la vue.
III-F-2. La fenêtre de visualisation (viewport)
III-F-2-a. Théorie
La fenêtre de visualisation est la portion de la zone cliente sur laquelle OpenGL va projetter la scène. Il ne faut pas la confondre avec la sortie OpenGL qui est toujours tout le DC de la fenêtre.
La fonction permettant de définir la fenêtre de visualisation est glViewport.
void glViewport(GLint x, GLint y, GLsizei width, GLsizei height);
|
Sous Windows, les nombres sont exprimés en pixels et le point (0, 0) correspond au coin inférieur gauche de la fenêtre. Si vous voulez utiliser toute la zone cliente et que votre fenêtre
ne peut pas être redimensionnée, il est donc inutile d'appeler cette fonction mais il est cependant recommandé de toujours le faire pour des raisons de maintenabilité. Cela se fait typiquement juste une fois
dans le traitement du message WM_SIZE. Cela permet en plus également d'ajuster automatiquement la nouvelle surface à chaque redimensionnement si la fenêtre peut être redimensionnée.
III-F-2-b. Application
Il est temps à présent de retoucher à un peu de code. Nous allons juste ajouter un appel explicite à glViewport et dessiner ... une théière. Evidemment, nous n'allons pas dessiner notre théière avec les commandes de
bas niveau de OpenGL que nous n'avons pas encore de toute façon étudiées. Nous allons plutôt utiliser la fonction bien pratique glutWireTeapot de la GLUT bien sûr d'après son nom. Cette fonction dessine une théière
en fils de fer contrairement à glutSolidTeapot qui la dessine en surfaces pleines. La théière sera centrée au point origine du repère.
Le dessin en fils de fer est une pratique très utilisée en modélisation 3D pendant les sessions de tests et/ou de débogage. En effet, les objets
en surfaces pleines ne peuvent être bien appréciées qu'une fois toutes les conditions nécessaires pour une scène réaliste réunies. Enfin, pourquoi une théière, c'est tout simplement la tradition.
La fonction de dessin de théière de la GLUT prend un unique argument réel qui doit indiquer la taille relative de la théière. Si vous spécifiez 1.0, la théière sera dessinée dans sa taille par défaut et si vous spécifiez 2.0,
elle sera deux fois plus grande. Comme vous pouvez le constater, vous n'avez pas beaucoup de contrôle sur la théière à dessiner mais c'est pas grave, c'est même mieux, en effet cette théière n'existe que pour être utilisée en débogage,
elle doit donc pouvoir se dessiner de la manière la plus simple du monde.
Enfin, sachez que dans OpenGL, la couleur par défaut des objets est blanc.
Voici donc un exemple de programme affichant une théière en utilisant les paramètres de vue par défaut de OpenGL :
#include <windows.h>
#include <gl/glut.h>
struct {
struct {
HDC hDC;
HGLRC hRC;
} Window;
} MyApp;
BOOL InitFullScreenMode(int width, int height, int color_bits);
LRESULT CALLBACK WndProc(HWND hwnd, UINT message, WPARAM wParam, LPARAM lParam);
int oglSetupDC(HDC hdc);
void Reshape(int width, int height);
void UpdateOutput(void);
void oglDraw(void);
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow)
{
WNDCLASS wc;
HWND hWnd;
MSG msg;
RECT rect;
LONG width = 800, height = 600;
DWORD style = WS_POPUP;
BOOL FullScreen = TRUE, ScreenOk = FALSE;
int ret = 0;
SetRect(&rect, 0, 0, width, height);
wc.cbClsExtra = 0;
wc.cbWndExtra = 0;
wc.hbrBackground = (HBRUSH)(COLOR_WINDOW + 1);
wc.hCursor = LoadCursor(NULL, IDC_ARROW);
wc.hIcon = LoadIcon(NULL, IDI_APPLICATION);
wc.hInstance = hInstance;
wc.lpfnWndProc = WndProc;
wc.lpszClassName = "OpenGL Window Class";
wc.lpszMenuName = NULL;
wc.style = CS_HREDRAW | CS_VREDRAW;
RegisterClass(&wc);
if (FullScreen)
{
ScreenOk = InitFullScreenMode(width, height, 32);
if (!ScreenOk)
{
int reponse = MessageBox(
NULL,
"Impossible d'initialiser le mode plein écran.\n"
"Voulez-vous exécuter le programme dans une fenêtre normale ?",
"OpenGL",
MB_YESNO | MB_ICONQUESTION
);
FullScreen = (reponse == IDNO);
}
}
if (!FullScreen)
{
OffsetRect(&rect, (GetSystemMetrics(SM_CXSCREEN) - width) / 2, (GetSystemMetrics(SM_CYSCREEN) - height) / 2);
style = WS_BORDER | WS_CAPTION | WS_SYSMENU | WS_MINIMIZEBOX;
}
if (!FullScreen || ScreenOk)
{
BOOL done;
if (!FullScreen)
AdjustWindowRect(&rect, style, FALSE);
hWnd = CreateWindow(
"OpenGL Window Class", "OpenGL Window",
style,
rect.left, rect.top, rect.right - rect.left, rect.bottom - rect.top,
NULL, NULL, hInstance, NULL
);
ShowWindow(hWnd, nCmdShow);
done = FALSE;
while (!done)
{
if (PeekMessage(&msg, NULL, 0, 0, PM_REMOVE))
{
done = (msg.message == WM_QUIT);
if (!done)
{
TranslateMessage(&msg);
DispatchMessage(&msg);
}
}
else
{
UpdateOutput();
}
}
ret = (int)msg.wParam;
}
return ret;
}
LRESULT CALLBACK WndProc(HWND hwnd, UINT message, WPARAM wParam, LPARAM lParam)
{
PAINTSTRUCT ps;
switch(message)
{
case WM_CREATE:
MyApp.Window.hDC = GetDC(hwnd);
oglSetupDC(MyApp.Window.hDC);
MyApp.Window.hRC = wglCreateContext(MyApp.Window.hDC);
wglMakeCurrent(MyApp.Window.hDC, MyApp.Window.hRC);
break;
case WM_SIZE:
Reshape(LOWORD(lParam), HIWORD(lParam));
break;
case WM_PAINT:
BeginPaint(hwnd, &ps);
UpdateOutput();
EndPaint(hwnd, &ps);
break;
case WM_DESTROY:
wglMakeCurrent(NULL, NULL);
wglDeleteContext(MyApp.Window.hRC);
ReleaseDC(hwnd, MyApp.Window.hDC);
PostQuitMessage(0);
break;
default:
return DefWindowProc(hwnd, message, wParam, lParam);
}
return 0L;
}
int oglSetupDC(HDC hdc)
{
PIXELFORMATDESCRIPTOR pfd;
int iPixelFormat;
ZeroMemory(&pfd, sizeof(pfd));
pfd.nSize = sizeof(pfd);
pfd.nVersion = 1;
pfd.dwFlags = PFD_DRAW_TO_WINDOW | PFD_SUPPORT_OPENGL | PFD_DOUBLEBUFFER;
pfd.iPixelType = PFD_TYPE_RGBA;
pfd.cColorBits = 32;
iPixelFormat = ChoosePixelFormat(hdc, &pfd);
SetPixelFormat(hdc, iPixelFormat, &pfd);
return iPixelFormat;
}
void Reshape(int width, int height)
{
glViewport(0, 0, width, height);
}
void UpdateOutput(void)
{
oglDraw();
SwapBuffers(MyApp.Window.hDC);
}
void oglDraw(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glutWireTeapot(0.5);
}
BOOL InitFullScreenMode(int width, int height, int color_bits)
{
DEVMODE dm;
dm.dmSize = sizeof(dm);
dm.dmPelsWidth = width;
dm.dmPelsHeight = height;
dm.dmBitsPerPel = color_bits;
dm.dmFields = DM_PELSWIDTH | DM_PELSHEIGHT | DM_BITSPERPEL;
return ChangeDisplaySettings(&dm, CDS_FULLSCREEN) == DISP_CHANGE_SUCCESSFUL;
}
|
III-F-3. La projection
III-F-3-a. Introduction
La matrice de projection qui définit le volume de visualisation par défaut de OpenGL est une matrice adaptée aux dessins en 2D, pas à la 3D. Plus précisément, elle est adaptée au dessin d'objets 2D dans un monde 3D. C'est une projection dite orthographique.
Ce nom provient de l'orthogonalité qu'il y a entres les différents plans qui limitent (appelés plans de clipping) le volume de visualisation. Une des conséquences notables de ce type de projection est que si vous dessinez un objet à une position donnée, et que vous dessinez
ce même objet derrière, plus loin mais de sorte qu'il ne soit pas totalement caché, on constatera que les deux objets ont les mêmes dimensions. Or dans la réalité celui qui se trouve plus loin doit apparaître en plus petit. Pour avoir ce résultat,
il ne faut pas utiliser une projection orthographique mais une projection en perspective.
III-F-3-b. Projection orthographique
Utilisez la projection orthographique pour faire de la 2D. Cette projection est également appelée parallèle (à cause du parallélisme qu'il y a entres les plans) ou en perspective cavalière. Les fonctions permettant d'obtenir une projection orthographique sont :
void glOrtho(GLdouble xmin, GLdouble xmax, GLdouble ymin, GLdouble ymax, GLdouble zmin, GLdouble zmax);
void gluOrtho2D(GLdouble xmin, GLdouble xmax, GLdouble ymin, GLdouble ymax);
|
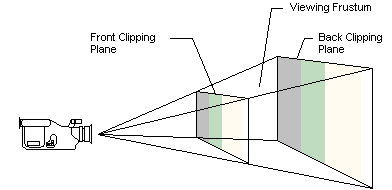
III-F-3-c. Projection en perspective
Dans une projection en perspective, le volume de visualisation de la caméra est un frustum pyramidique, c'est-à-dire une portion d'une pyramide partant de la caméra et "se propageant" dans le sens ou elle regarde, ce qui est une meilleure modélisation de la réalité.
La figure ci-dessous, tirée de la MSDN Library, illustre un tel volume.
Les fonctions permettant d'obtenir une projection en perspective sont :
void glFrustum(
GLdouble front_left, GLdouble front_right, GLdouble front_bottom, GLdouble front_top,
GLdouble front_distance, GLdouble back_distance
);
void gluPerspective(
GLdouble fovy, GLdouble aspect,
GLdouble front_distance, GLdouble back_distance
);
|
La seule différence entre glFrustum et gluPerspective ce sont les paramètres qu'il faut les passer. Une implémentation perso de gluPerspective (ici vraiment naïve) vous aiderait à comprendre :
void glu_perspective(GLdouble fovy, GLdouble aspect, GLdouble front_distance, GLdouble back_distance)
{
GLdouble fovx = fovy * aspect;
GLdouble front_height = 2 * front_distance * tan(DEG_TO_RAD(fovy /2));
GLdouble front_width = 2 * front_distance * tan(DEG_TO_RAD(fovx /2));
glFrustum(-front_width / 2, front_width / 2, -front_height / 2, front_height / 2, front_distance, back_distance);
}
|
Ces fonctions ne font que multiplier la matrice courante par une matrice décrivant la transformation cherchée. D'habitude, vous sélectionnerez donc la matrice de projection et la réinitialiserez
à la matrice identité avant d'appeler une de ces fonctions. Sachez également que front_distance et back_distance doivent toujours être strictement positifs.
Dans la suite, nous utiliserons la plupart du temps une projection en perspective. Notre nouvelle fonction Reshape est :
void Reshape(int width, int height)
{
GLint prev_matrix;
glViewport(0, 0, width, height);
glGetIntegerv(GL_MATRIX_MODE, &prev_matrix)
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, ((GLdouble)width) / height, 0.1, 10.0);
glMatrixMode(prev_matrix);
}
|
III-F-3-d. La correction de perspective
En fait, les fonctions glFrustum et gluPerspective ne servent qu'à définir un volume de visualisation convenable (le frustum) pour une projection en perspective. Demander à OpenGL de projeter de manière réaliste les objets lors d'une vue en perspective,
c'est une autre histoire. Pour cela, il faut explicitement à OpenGL de faire des corrections ("hints") de perspective, ce qui réclame plus de calculs, c'est pourquoi cette fonctionnalité est initialement désactivée. Pour activer la correction de perspective,
exécutez glHint(GL_PERSPECTIVE_HINT, GL_NICEST). Les autres valeurs possibles à la place de GL_NICEST (meilleure correction possible) sont GL_FASTEST (correction la plus rapide) et GL_DONTCARE (ne pas faire de correction),
la valeur par défaut. Nous verrons d'autres utilisations de glHint au fur et à mesure de nos besoins.
En ce qui concerne la suite de ce tutoriel, nous allons définir une fonction
III-F-4. Le repère
Dans OpenGL, le repère n'est pas attaché à l'espace. Lorsque vous déplacez le repère par exemple, vous ne déplacez avec ni les objets déjà placés ni la caméra, seulement le repère. Pour appliquer une transformation au repère, il suffit de multiplier
la matrice de changement de repère par la matrice de la transformation que vous voulez appliquer. Par exemple, pour déplacer le repère d'un vecteur (0, 0, -1), il suffit de multiplier la matrice de changement
de repère par la matrice de translation de vecteur (0, 0, -1). Mais rassurez-vous, il est très possible que vous n'aurez même pas à composer "à la main" une seule matrice de toute votre vie. Vous devez juste savoir
qu'une transformation 3D se fait par multiplication par une matrice 4 x 4.
Vous rappelez-vous de la position initiale du repère par rapport à la caméra ? C'est la position du repère,
par rapport à la cam, lorsque la matrice de changement de repère est égale à la matrice identité. En modifiant cette matrice, vous dépacez/déformez ce repère. Pour revenir à l'état initial, remettez la matrice de changement de repère
à la matrice identité. En résumé, on peut donc dire que la matrice de changement de repère n'est rien d'autre que la matrice de la transformation totale qu'a subi le repère par rapport à son état initial.
Il existe des fonctions utilitaires permettant d'effectuer des transformations simples de repère sans avoir à faire explicitement les multiplications de matrices. Il s'agit de "glTranslate", "glRotate" et "glScale".
void glTranslatef(GLfloat x, GLfloat y, GLfloat z);
void glTranslated(GLdouble x, GLdouble y, GLdouble z);
void glRotatef(GLfloat a, GLfloat x, GLfloat y, GLfloat z);
void glRotated(GLdouble a, GLdouble x, GLdouble y, GLdouble z);
void glScalef(GLfloat k_x, GLfloat k_y, GLfloat k_z);
void glScaled(GLdouble k_x, GLdouble k_y, GLdouble k_z);
|
Par exemple, pour afficher la théière dans une autre position qu'au centre de la fenêtre, il suffit de faire déplacer le repère jusqu'au centre voulu avant de la dessiner. Il faut, avant de faire la transformation du repère, le réinitialiser afin que la transformation ne
se cumule pas à chaque appel de oglDraw. Par exemple :
void oglDraw(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(-1.0f, 0.0f, 0.0f);
glutWireTeapot(0.5);
}
|
Vous pouvez aussi remplacer glTranslatef(-1.0f, 0.0f, 0.0f) par deux glTranslatef(-0.5f, 0.0f, 0.0f) par exemple, mais l'intérêt est effectivement limité.
III-F-5. Tout est relatif
III-F-5-a. Le repère et les objets
Nous avons vu que lorsque nous déplaçons le repère par exemple, cela ne déplace pas les objets dessinés. Après le changement de repère,
les objets qui ont déjà été placés, y compris la caméra, changent par contre donc de coordonnées. En conclusion, changer de répère est strictement équivalent,
sans aucune exception, à faire bouger tous les objets déjà dessinés. Par exemple, lorsque vous demandez l'exécution de : "Déplacer le repère d'un
vecteur de translation égal à (1, 0, 0)", vous auriez également pu la formuler ainsi : "Déplacer tous les objets déjà placés, y compris la caméra, d'un vecteur de
translation égal à (-1, 0, 0)". Il est cependant recommandé de toujours orienter ses pensées vers les transformations de repère plutôt que vers les transformations
des objets en place.
III-F-5-b. Le repère et la caméra
Dans OpenGL, la caméra est toujours être fixe. On ne peut changer ni sa position, ni son orientation, ni son zoom. Il existe cependant un cas particulier dans lequel vous aurez l'impression
de pouvoir changer librement la position, l'orientation ou le zoom de la caméra : c'est quand votre univers est encore vide, c'est-à-dire tant que vous n'avez encore rien dessiné. En effet, tant que
votre scène est vide, il n'y a aucune différence entre déplacer la caméra d'un vecteur de translation égal à (-1, 0, 0) par exemple et déplacer le repère du vecteur de translation
opposé. Dès qu'un objet a été placée sur la scène, l'équivalent du déplacement de la caméra devient le déplacement (inverse) du repère ET de tous les objets déjà placés, pas le déplacement du repère
uniquement. Or cela ne se fait pas de manière aisée. De toute façon, on a rarement (pour ne pas dire jamais) besoin de modifier les paramètres de la caméra en dehors de l'initialisation de la scène.
Dans ce tutoriel, nous ne discuterons même pas (et nous n'en aurons jamais besoin) des techniques permettant de se créer l'illusion de pouvoir modifier les paramètres de la caméra à n'importe quel moment
parce que c'est inutilement compliqué, ce n'est pas si important que cela, et que si vous suivez bien ce tutoriel, vous comprendrez la technique vous-même.
La GLU forunit la fonction gluLookAt qui permet de multiplier la matrice courante M par une matrice de transformation T de sorte que si M est la matrice de changement de repère, qu'elle
soit égale à la matrice identité et que la scène soit encore vide, cette transformation soit équivalente à un paramétrage de la caméra conformément aux paramètres passés.
void gluLookAt(
GLdouble eyex, GLdouble eyey, GLdouble eyez,
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz
);
|
Eye est le point où l'on veut placer la caméra, Center le point vers lequel on veut que la caméra soit tournée et Up un vecteur indiquant la direction pointée par le haut de la tête du caméraman.
Retenez bien que gluLookAt ne fait que multiplier la matrice courante par une matrice de transformation provoquant la transformation du repère équivalente, c'est-à-dire en combinant tout simplement des "glTranslate"
et des "glRotate". Si vous voulez placer la caméra à une position relative au repère initial et non relative au repère courant, réinitialisez la matrice GL_MODELVIEW avant de la multiplier en appelant gluLookAt.
III-G. Dessiner
III-G-1. Généralités
III-G-1-a. Les vertices
Dans OpenGL, la base de tout dessin sont ce qu'on appelle les vertices (au singulier : vertex). Un vertex, ou encore sommet même si vertex est la plupart du temps le terme approprié, est tout simplement un point ou un point de contrôle.
Par exemple pour dessiner un triangle ABC, il faut trois vertices : les points (vertices) A, B et C. Voici un exemple de code permettant de dessiner un triangle plein. Utilisons une projection orthographique pour bien apprécier le résulat.
void oglDraw(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_TRIANGLES);
glVertex3f(0.0f, 0.0f, 0.0f);
glVertex3f(0.5f, 0.0f, 0.0f);
glVertex3f(0.0f, 0.5f, 0.0f);
glEnd();
}
|
Certaines commandes OpenGL, glVertex par exemple, existent sous plusieurs formes, cela n'est d'ailleurs pas nouveau pour nous. Le format général des commandes est : glFunctionName[n][u][t][v].
- n indique le nombre de paramètres qu'on veut passer. Lorsqu'il est présent, peut être égal à 1, 2, 3 ou 4.
- u indique que les paramètres sont non signés (unsigned)
- t indique le type des paramètres. Lorsqu'il est présent, peut être b : byte, s : short, i : int, f : float ou d : double
- v indique que les n paramètres sont passés via un tableau
Des noms valides sont donc par exemple : glVertex2f, glVertex2i, glVertex3fv, glVertex4d, etc.
Dans "glVertex", n et t sont toujours présents. n peut être égal à 2, 3 ou 4. Vous-vous demandez sûrement ce que c'est que ce quatrième paramètre. Et bien, dans OpenGL chaque vertex possède 4 composantes :
(x, y, z, w). Pourquoi en faut-il 4 ? Parce que lorsque vous changez de repère, OpenGL va placer les objets que vous dessinez en se basant sur le nouveau repère, ça vous le savez. Vous savez également que
la matrice de changement de repère, que nous allons noter M, peut être interprétée comme étant la matrice de la transformation totale qu'a subi le repère original. Considérons le point A dont les coordonnées sont (x, y, z) dans le nouveau
repère. Pour pouvoir placer ce point, OpenGL doit d'abord calculer les coordonnées de ce point dans le repère original, le seul repère que OpenGL connaît ! Pour faire cela, il suffit de multiplier M par "(x, y, z)".
Le problème est que M est une matrice de dimensions 4 x 4, elle ne peut pas être multipliée par une matrice 3 x 1. Il faut donc ajouter une quatrième composante, afin d'obtenir une matrice 4 x 1 qui peut enfin multiplier les
matrices d'OpenGL. Mais que mettre alors dans la 4ème composante ? 1 ! C'est presque une règle. En effet, certaines transformations ne se font pas correctement si la valeur de cette composante n'est pas 1. Prenons le cas d'un repère translaté d'un vecteur (tx, ty, tz) par exemple.
Si (x, y, z) sont les coordonnées d'un point A dans le repère courant, ses coordonnées (a, b, c) dans le repère original sont données par :
[a] [1 0 0 tx] [x] [x + w*tx]
[b] = [0 1 0 ty] x [y] = [y + w*ty]
[c] [0 0 1 tz] [z] [z + w*tz]
[d] [0 0 0 1 ] [w] [ w ]
|
On voit donc très bien que les translations ne fonctionneront correctement que si chaque point a la valeur 1 à la composante w. Dans "glVertex", quand w n'est pas spécifiée, elle aura la valeur 1. Quand z n'est pas spécifiée, elle aura la valeur 0.
III-G-1-b. Les couleurs
Dans OpenGL, la couleur par défaut utilisée pour dessiner les objets est le blanc. Pour choisir la couleur courante (GL_CURRENT_COLOR), on peut utiliser la fonction "glColor" en spécifiant les paramètres R, G et B (ex : glColor3f) ou R, G, B, et A (ex : glColor4f).
Nous ne parlerons pas encore cependant du paramètre alpha. Plutôt, voici un exemple de code permettant de dessiner un triangle en bleu.
void oglDraw(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f, 0.0f, 1.0f);
glBegin(GL_TRIANGLES);
glVertex3f(0.0f, 0.0f, 0.0f);
glVertex3f(0.5f, 0.0f, 0.0f);
glVertex3f(0.0f, 0.5f, 0.0f);
glEnd();
}
|
En fait, dans OpenGL, les couleurs sont attribuées aux sommets. Chaque fois que vous créez un sommet, ce dernier sera colorié avec la couleur courante. OpenGL effectue automatiquement une interpolation pour calculer la couleur des autres points comme vous pouvez le constater grace à cet exemple :
void oglDraw(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_TRIANGLES);
glColor3f(1.0f, 0.0f, 0.0f);
glVertex3f(0.0f, 0.0f, 0.0f);
glColor3f(0.0f, 1.0f, 0.0f);
glVertex3f(0.5f, 0.0f, 0.0f);
glColor3f(0.0f, 0.0f, 1.0f);
glVertex3f(0.0f, 0.5f, 0.0f);
glEnd();
}
|
III-G-1-c. Le test de profondeur
Considérons le code suivant :
void oglDraw(void)
{
GLfloat h = 0.866f ;
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_TRIANGLES);
glColor3f(1.0f, 0.0f, 0.0f);
glVertex3f(-0.5f, 0.0f, 0.5f);
glVertex3f(0.5f, 0.0f, 0.5f);
glVertex3f(0.0f, h, 0.5f);
glColor3f(0.0f, 0.0f, 1.0f);
glVertex3f(-0.5f, 0.0f, -0.5f);
glVertex3f(0.5f, 0.0f, -0.5f);
glVertex3f(0.0f, h, -0.5f);
glEnd();
}
|
Contrairement à vos attentes, cela ne va pas faire apparaître le triangle rouge, qui est normalement au premier plan,
mais le triangle bleu, parce que c'est le dernier objet dessiné. Chaque nouveau dessin écrase tout dessin déjà fait. Pour
demander à OpenGL d'effectuer un test correct de profondeur, exécutez, idéalement lors des phases d'initialisation,
la commande glEnable(GL_DEPTHTEST). Mais ce n'est pas fini ...
Lorsque vous avez activé le test de profondeur, vous devez, à chaque actualisation de la scène, réinitialiser le depth buffer
comme vous devez toujours à ce moment réinitialiser le color buffer. Nous avons déjà vu que cela est nécessaire pour avoir une
projection correcte. Lors de la réinitialisation de la scène donc, vous devez exécuter glClear(GL_COLOR_BUFFER_BIT | GL_COLOR_DEPTH_BIT)
et non plus glClear(GL_COLOR_BUFFER_BIT) uniquement.
OpenGL fait correspondre à tout point du volume de visualisation un indice de profondeur.
Les valeurs normalisées sont 0.0 pour indiquer un point le proche possible de la caméra (c'est-à-dire un point du plan de clipping "front") et
1.0 pour indiquer un point le plus éloigné possible (c'est-à-dire un point du plan de clipping "back"). Vous pouvez spécifiez la valeur à utiliser
par glClear pour réinitialiser le depth buffer à l'aide de la fonction glClearDepth. Tant que vous ne l'avez pas appelée, la valeur est 1.0
ce qui signifie que lorsque vous réinitialisez le buffer, tous les fragments sont replacés sur le plan le plus reculé du volume de visualisation
à savoir le plan de clipping "back", ce qui correspond souvent à nos attentes.
Une fois le test de profondeur activé, le fragment retenu pour un pixel donné sera par défaut celui qui est le plus proche de la caméra.
Ainsi, en activant le test de profondeur, on obtiendra enfin à l'écran, avec notre code précédent, le triangle rouge et non le triangle bleu.
Vous pouvez spécifier comment OpenGL doit choisir le fragment à retenir pour un pixel donné lors du test de profondeur à l'aide de la fonction
glDepthFunc. Par défaut, lorsque le test de profondeur est activé, la règle utilisée est GL_LESS (glDepthFunc(GL_LESS)). Cela signifie
que c'est le fragment qui aura l'indice de profondeur le plus faible qui sera retenu. Nous verrons les autres règles utilisables au fur et à mesure de
nos besoins. Dans toute la suite, nous allons toujours activer le test de profondeur. Comme il peut y avoir d'autres initialisations de ce genre
(par exemple activation de la correction de perspective, etc.), le mieux est que nous introduisions une nouvelle fonction - oglInit - à l'intérieur
de laquelle nous mettrons toutes les initialisations requises par nos programmes, et que nous appelerions à la fin de toutes les autres initailisations
(GetDC, wglCreateContext, etc.). Voici une version minimale :
void oglInit(void)
{
glEnable(GL_DEPTH_TEST);
}
|
III-G-2. Les primitives
III-G-2-a. Points (GL_POINTS)
Dessine des points. Le code suivant dessine 3 points : A, B et C.
void oglDraw(void)
{
GLfloat A[] = {0.0f, 0.0f, 0.0f};
GLfloat B[] = {0.5f, 0.0f, 0.0f};
GLfloat C[] = {0.0f, 0.5f, 0.0f};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_POINTS);
glVertex3fv(A);
glVertex3fv(B);
glVertex3fv(C);
glEnd();
}
|
Bien qu'il soit possible de spécifier le diamètre, en pixels, d'un point à l'aide de glPointSize, il est recommandé de ne dessiner que des points de diamètres égales à 1.0,
le diamètre par défaut. Une des principales raisons est qu'à partir d'une certaine valeur vous obtiendrez quelque chose qui ressemble plus à un cuble qu'à un point. Si vous
vous voulez dessiner un "gros point", dessinez carrément une sphère. Nous y reviendrons plus tard.
Vous pouvez améliorer l'apparence de vos points en activant le lissage (ou anticrénelage ou, en anglais, antialiasing). Le lissage est une technique qui permet d'obtenir des images aux contours lisses,
c'est-à-dire pas trop pixélisées, d'où son nom. Pour activer le lissage des points, exécutez la commande glEnable(GL_POINT_SMOOTH). Ensuite pour utiliser la meilleure correction possible, ce que vous devez la plupart du temps toujours faire,
exécutez glHint(GL_POINT_SMOOTH_HINT, GL_NICEST).
III-G-2-b. Lignes (GL_LINES, GL_LINESTRIP et GL_LINE_LOOP)
GL_LINES dessine des lignes. Le code suivant dessine 2 lignes (des segments) : [AB] et [CD].
void oglDraw(void)
{
GLfloat A[] = {-0.5f, 0.5f, 0.0f};
GLfloat B[] = {0.5f, -0.5f, 0.0f};
GLfloat C[] = {-0.5f, -0.5f, 0.0f};
GLfloat D[] = {0.5f, 0.5f, 0.0f};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_LINES);
glVertex3fv(A);
glVertex3fv(B);
glVertex3fv(C);
glVertex3fv(D);
glEnd();
}
|
Bien qu'il soit possible de spécifier le diamètre, en pixels, d'une ligne à l'aide de glLineWidth, il est recommandé de ne dessiner que des lignes de diamètres égales à 1.0,
le diamètre par défaut. En outre, vous améliorerez nettement l'apparence de vos lignes en activant le lissage des lignes, en exécutant tout simplement la commande
glEnable(GL_LINE_SMOOTH). Ensuite pour utiliser la meilleure correction possible, ce que vous devez la plupart du temps toujours faire,
exécutez glHint(GL_LINE_SMOOTH_HINT, GL_NICEST).
GL_LINE_STRIP dessine des lignes connectées. Avec GL_LINESTRIP au lieu de GL_LINES, le code ci-dessus donnerait donc une courbe composée des segments [AB], [BC] et [CD].
GL_LINE_LOOP est semblable à GL_LINE_STRIP sauf que cette fois-ci la courbe sera fermée. Avec GL_LINE_LOOP au lieu de GL_LINES, le code ci-dessus donnerait donc une courbe
composée des segments [AB], [BC], [CD] et [DA].
III-G-2-c. Polygones
III-G-2-c-i. Cas général : GL_POLYGON
OpenGL ne permet de dessiner que des polygones convexes. Pour rappel, un polygone est dit convexe lorsque pour tous points A et B de la surface du polygone, tous les points
du segment [AB] appartiennent également au polygone. Pour dessiner un polygone non convexe, vous devez superposer des polygones convexes. GL_POLYGON permet de dessiner un polygone convexe.
Les triangles (polygones à trois côtés) et les quadrilatères (polygones à 4 côtés) sont juste des cas particuliers de polygones convexes.
Par défaut, les polygones que vous dessinez sont des surfaces. En effet, si vous vouliez dessiner des courbes ou des points représentant un polygone, vous auriez la plupart du temps mieux fait d'utiliser tout
simplement GL_LINE_LOOP ou GL_POINTS par exemple. Néanmoins, OpenGL fournit la glPolygonMode qui permet de spécifier comment vous voulez dessiner vos polygones.
void glPolygonMode(GLenum face, GLenum mode);
|
Le paramètre face indique la face dont vous voulez changer la manière de le dessiner. Vous pouvez spécifier GL_FRONT pour modifier la façon dont OpenGL dessinera les faces avant de vos polygones,
GL_BACK pour les faces arrières et GL_FRONT_AND_BACK (par défaut) pour appliquer le mode pour les deux faces. Le paramètre mode indique comment dessiner les faces indiquées à l'aide du paramètre face.
GL_POINT indique que vous voulez dessiner juste les sommets, GL_LINE que vous voulez juste dessiner le contour et GL_FILL (par défaut) que vous voulez dessiner des polygones pleins,
c'est-à-dire des surfaces. Nous approfondirons la notion de face plus tard. Pour le moment, contentez-vous de toujours utiliser GL_FRONT_AND_BACK.
Pour activer le lissage des polygones, exécutez glEnable(GL_POLYGON_SMOOTH). Ensuite pour utiliser la meilleure correction possible, ce que vous devez la plupart du temps toujours faire,
exécutez glHint(GL_POLYGON_SMOOTH_HINT, GL_NICEST).
III-G-2-c-ii. GL_TRIANGLES
Dessine des triangles. Nous avons déjà vu des exemples d'utilisation.
III-G-2-c-iii. GL_TRIANGLE_STRIP
Dessine des triangles liés, par zig-zag. L'exemple suivant dessine 3 triangles : ABC, BCD et CDE.
void oglDraw(void)
{
GLfloat A[] = {-0.5f, 0.0f, 0.0f};
GLfloat B[] = {-0.5f, 0.5f, 0.0f};
GLfloat C[] = {0.0f, 0.0f, 0.0f};
GLfloat D[] = {0.5f, 0.5f, 0.0f};
GLfloat E[] = {0.5f, 0.0f, 0.0f};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_LINES);
glVertex3fv(A);
glVertex3fv(B);
glVertex3fv(C);
glVertex3fv(D);
glVertex3fv(E);
glEnd();
}
|
III-G-2-c-iv. GL_TRIANGLE_FAN
Dessine des triangles liés, ayant comme vertex commun le premier vertex. L'exemple suivant dessine 3 triangles : ABC, ACD et ADE.
void oglDraw(void)
{
GLfloat A[] = {0.0f, 0.0f, 0.0f};
GLfloat B[] = {0.5f, 0.0f, 0.0f};
GLfloat C[] = {0.5f, 0.5f, 0.0f};
GLfloat D[] = {-0.5f, 0.5f, 0.0f};
GLfloat E[] = {-0.5f, 0.0f, 0.0f};
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_LINES);
glVertex3fv(A);
glVertex3fv(B);
glVertex3fv(C);
glVertex3fv(D);
glVertex3fv(E);
glEnd();
}
|
III-G-2-c-v. GL_QUADS
Dessine des quadrilatères. Usage très semblable à GL_TRIANGLES.
III-G-2-c-vi. GL_QUAD_STRIP
Equivalent de GL_TRIANGLE_STRIP pour les quadrilatères.
III-G-3. Conclusion
Avec les primitives simples (triangles, quadrilatères, etc.), il est possible de dessiner n'importe quel objet tridimensionnel, aussi complexe soit-il. Généralement, le motif utilisé pour constituer l'image 3D est fixe
(par exemple, toujours un quadrilatère). Cette technique de construction d'un objet 3D à partir d'un même motif simple est appelée la tesselation.
En pratique, pour une forme très complexe, vous allez rarement la programmer directement, à partir de rien, vous-même.
Vous allez plutôt la dessiner à l'aide d'un modeleur 3D (comme 3ds max, blender, etc.), l'enregistrer dans un fichier puis charger ce fichier pour en extraire, fondamentalement, les vertices la constituant et enfin,
réellement la dessiner. L'étude détaillée de ces différentes étapes dépassent largement le cadre de ce tutoriel, mais vous devez tout simplement savoir qu'il est hors de question que vous allez
à chaque fois tout programmer, sauf si c'est juste pour le fun, pas pour une application à développer sous des contraintes de temps. Un objet tridimensionnel stockable dans un fichier et réutilisable par la suite
est appelé un mesh.


Les sources présentées sur cette page sont libres de droits
et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation
constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright ©
2010 Melem. Aucune reproduction, même partielle, ne peut être
faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.